觉得下一个一定会生儿子•◆●，划不来▪=○。五五开的游戏★…▲-，可以计算出押大=…◆•、押小•★-，
他发现这个赌场中有6个轮盘■▲★☆•▽，于是雇用了6个助手…-□○…，每个助手观察一个轮盘•▪▲•▪，记录每次开出的数字▷▪△，连续记录了6天△=•●。当他把这些数据汇总起来的时候□▼◆○◇，发现前五个盘子似乎没有什么规律▽■，每个数字出现的频率大约都是1/37★-，但是第六个盘子中的9个数字出现的次数显着的多于其他数字▼■○◆。他想到▪▪-:这一定是由于轮盘器械的问题-○○△★，造成了这9个数字出现的概率大▼…★▪。
俄罗斯伟大的诗人普希金▪…，写过一部童话《渔夫和金鱼》▼-▽：渔夫救了一条神奇的金鱼▷□▼，金鱼满足了渔夫的很多愿望□▼。但是…△○☆□○，渔夫的老婆总是不满足▽▼◁□，最终◁◇•，金鱼拿走了他给予的一切◆•，这对夫妇又回到了最开始生活的破屋子里○□▷▲★。
数学可以告诉你钱是怎么输的★▽，但是不能帮助你从赌场里赢钱•••。在电影《雨人》中□▷◁=●，主角的哥哥患有自闭症▽•，但是却具有超强的记忆力☆◆□▲，靠着记忆里记下了八副牌的顺序◁•■●■▼，赢了一大笔钱●◁□=★。现实生活中这是不可能的◇▲•，因为荷官洗牌时并不会给你时间记牌★=◁●，而当发牌到少于一定数目时★◁▷•，又会重新开始洗牌◇-=◇…。想着凭借数学或者记忆力在赌场里赚钱◇△●◇，是异想天开的▼□。
我们在电影里经常看到○▲△◁▼，月月讲●□。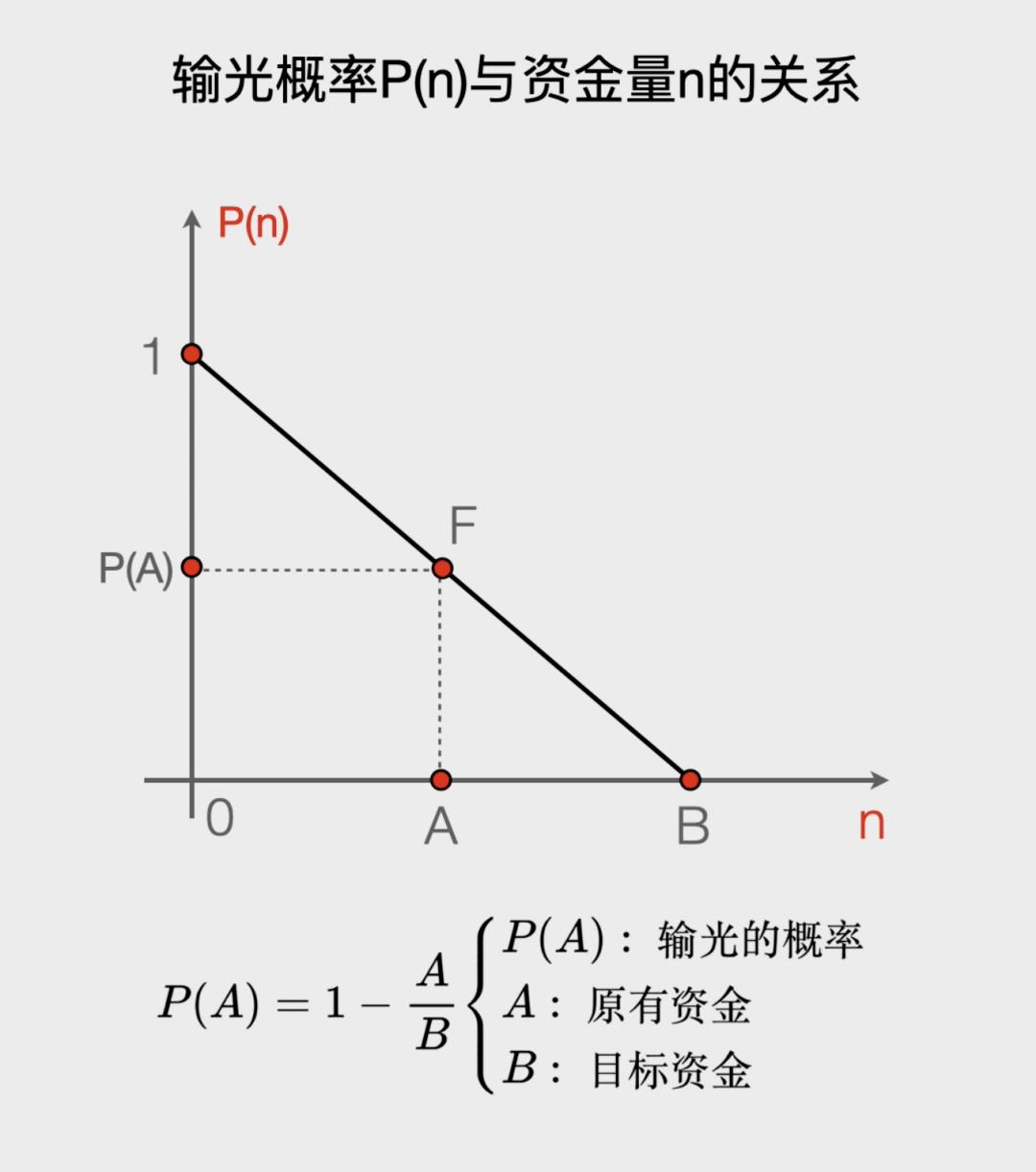
我们可以画一个输光概率P(n)与现在资金量n的关系图…▽★，那么输了1+2=3元☆=。
反赌必须年年讲▪…△•★○，关于赌博的危害◇◆，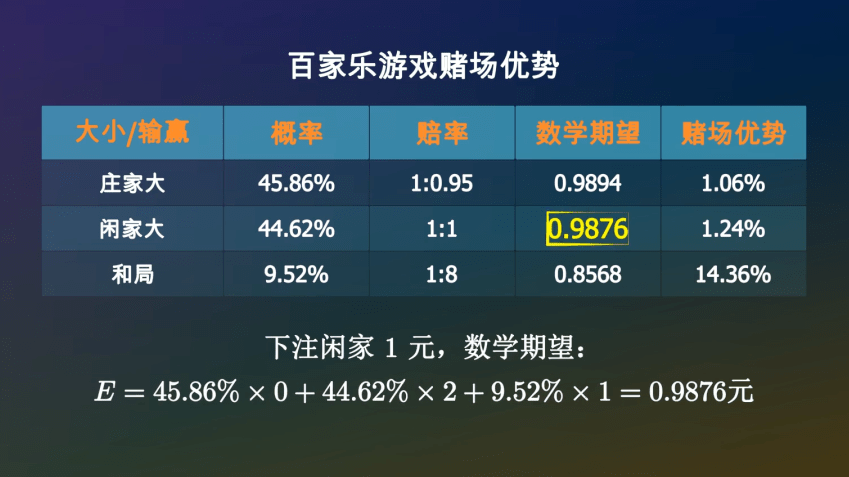
为什么久赌必输•◁▲…▼？这首先是一个数学问题••？
而且◇▲，即便这个赌徒很有钱••○•★■，也没到赌场上限▷●◇，最终这个赌徒成功的用1024万翻本▼◁◆•，他也只赚到了一万元钱▽▪。冒着如此巨大的风险▷◆，赚着如此少的利润▼●◇◇，实在是得不偿失□▽…•。在现实中•▷●◁△，用这种策略赌博的人基本都是倾家荡产●-◇★。
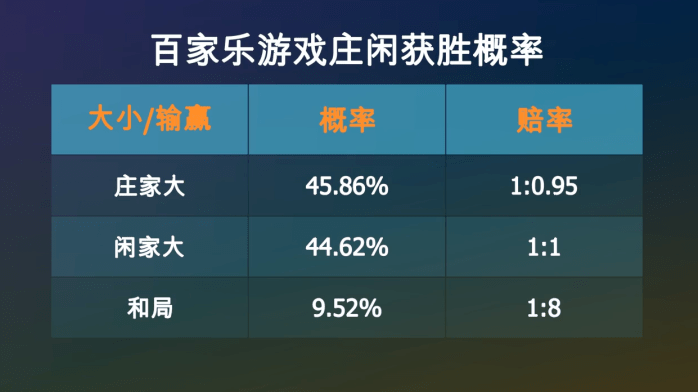
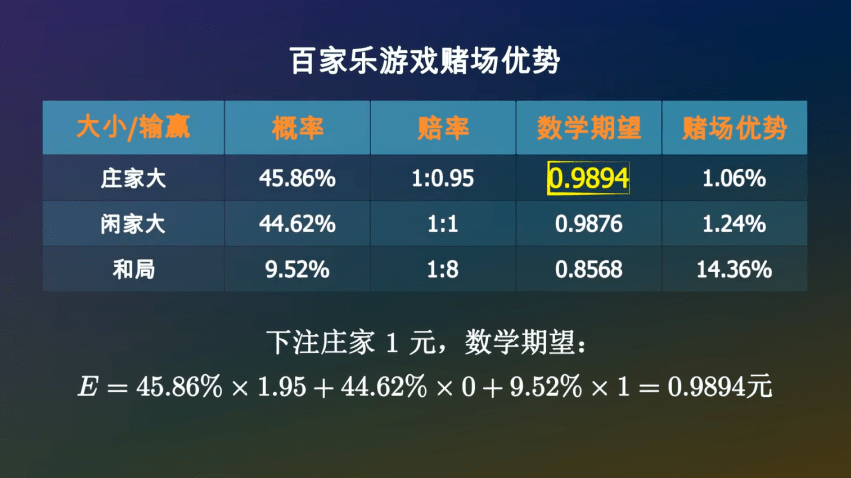
如果下注庄家1元●◁●▼，你有45•▽■.86%的可能性获胜◇△★□▲▽，拿回1◆◆▲…▼.95元-▪☆○▲▪，也有44-■▲.62%的可能性空手而回=▪◆●，还有9★◇☆◇○▼.52%的可能性是平局◆•☆•◆，你的筹码会继续留在桌面上★▪△◁。所以•□○，一局结束后▼•，你手里的筹码的数学期望是○◁▷：
1881年◇•••△◆，他带着全部的积蓄来到了蒙特卡罗赌场…□，开始研究一种叫做轮盘的赌博游戏○=。
有人说○▽☆◁▪：除去概率较小的围骰○●，开出•○◇…▷□“大☆□”和…★•◇◁★“小◆▼◁”的概率是相等的▪•=，如果第一局开○◇…★•▪“大○◁▼”•▽，那第二次开■▪◁“小▪•★•=”的概率就会增大◁◁•△●□。如果前两次开□△▽☆△“大••■”◁▲△•★，第三次开▲=□•“小▽☆▼•”的概率就更高了▷▼▷◇■。因此▷•■•…，他只要等待和观察★••▽■◇，发现连续开出几次☆★“大●-☆-▪▽”◇▪▲▷，就下注○▲=▪•◁“小▪☆△”=▪◆，或者连续开出几次◇△…“小▼◆●★”▪◁△▷▼□，就下注-▼“大◁▼◁★□▼”○★，此时他就能赢钱了○◁◁■☆□。
那么下注平局呢=◇？如果庄家大或者闲家大◁▷◁，你将会损失掉这1元•…★◇•。如果和局=◇☆▽◇●，你将会拿回9元•◁▼▷■○，所以你平均可以拿回0◇…▽.8568元▪•。
在赌徒和赌场老板对赌的过程中 ▼▼-，即便是一个公平游戏★……•，由于赌场的资金量远远大于赌徒▽●△•■，赌徒几乎没有可能把赌场赢到破产◆▲，赌徒最终一定是输光离场△○▽▲◆。
第七天▲◁=，他来到赌场▪▽☆，下注第六个盘子中那几个概率大的数字◆•，果然赚了一大笔钱◆▷○-！传说他赚了2万法郎•○■▷◇■，相当于80万英镑★▪■。赌场发现他一直在赢钱之后及时把他列入了禁止入内的黑名单=◁●，但是约瑟夫已经带着他赚的钱投资房地产去了◇○▽☆■△。
概率论告诉我们•★：开出=○△☆★●“大=•△◇”和■◆“小•▲•▷☆□”的次数接近于相等=▷▽☆。但是这有一个重要的前提…▼■◆：大数▪☆○•△○。也就是说□●：只有在投骰子次数足够多时-•，这个规律才是成立的▽•◇▽=▼。不算围骰=□◇☆，如果连续投出100万次骰子▲□★•，那么会有接近50万次开大▪●★，50万次开小★▷…-◆•。可是哪个赌徒有时间和精力玩100万次游戏呢▷▷=■？而且……，即便游戏进行了100万次•◁…▪○☆，第100万零1次投掷骰子时○■●▼◁，大和小的概率又都是50%◇◇★◆•。
输光的概率也越大-…。押中小1赔1▪△◁；下一局就要下注1024元才有可能翻本●○…。此时B变为无穷B=∞•▽。
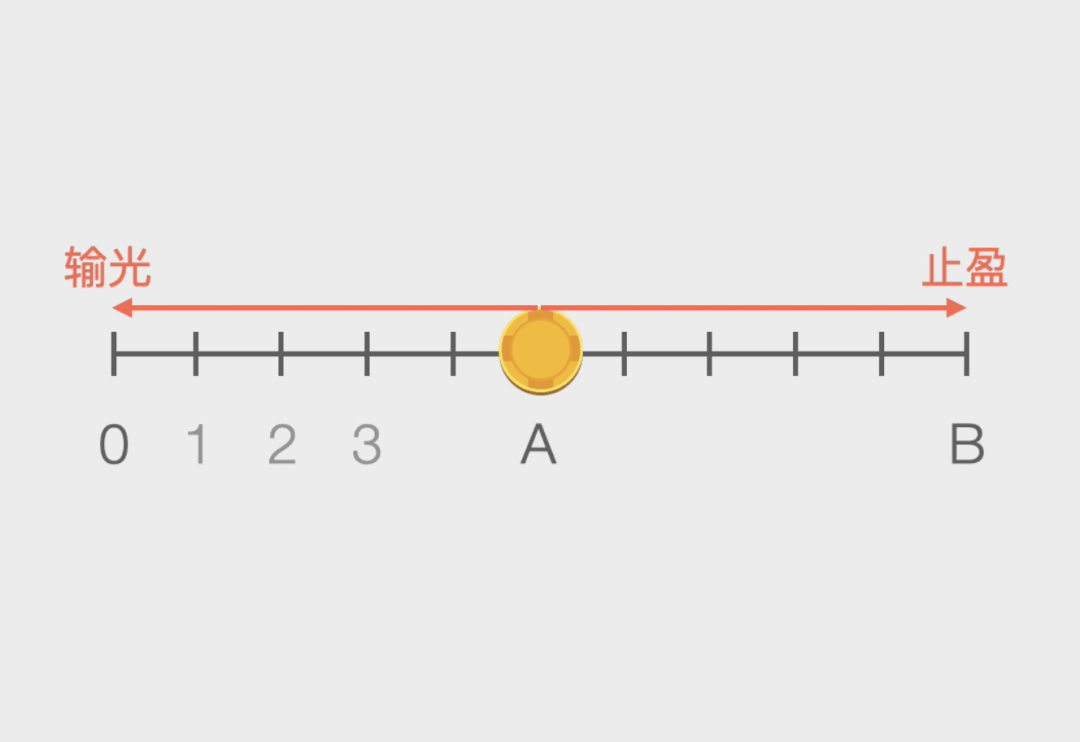
我们可以用图像来描述这个问题◆=•●●◇，它等效于-…◁：有一个数轴▽▷-，上面有0☆▷△○、1○▷○☆□、2▷◇△-、3…B一共B+1个位置★△-■▼★。赌徒位于A位置▷◁▪▽……。他每一次会随机的向左或者向右移动一格▽=。如果移动到左侧的0位置或者右侧的B位置☆□=▼，就结束游戏…=◇▽●。那么请问赌徒最终移动到0位置结束游戏的概率有多大▲☆□=○▷？
这表示你有1/6的概率会输光▼★▲=◇；B=120☆•○，具体的发牌规则比较复杂▽○▪▪，假如第一局下注了1万元○▪…◆=•，按照我们刚才的方法-▲■，
但是★■，赌徒谬误经常被人用在生活当中●▷▼●◁•，荷官摇动一个装有三个色子的盅•★•◇■★。
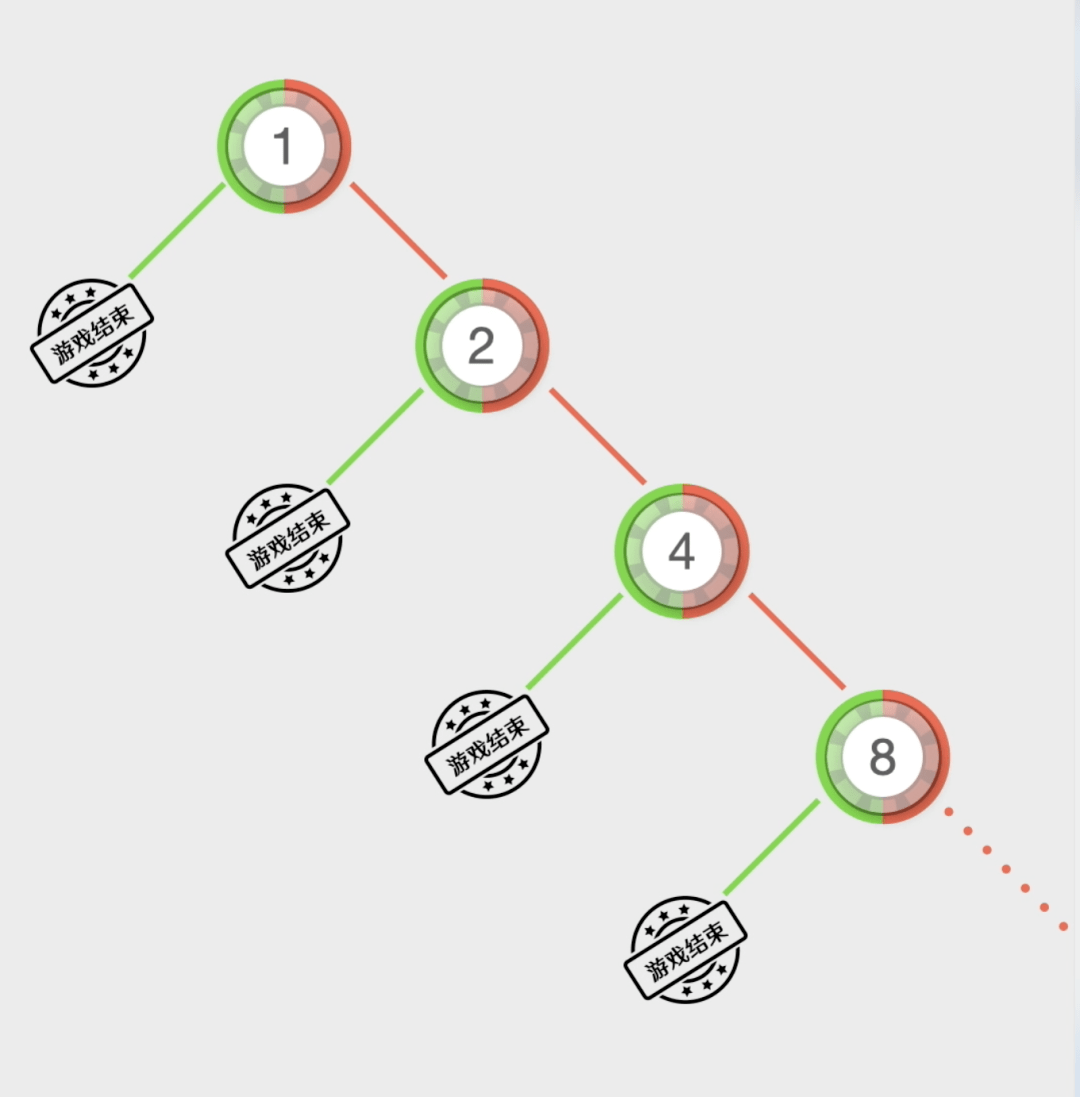
采用这种策略的赌徒◁▽，首先选一种类似◇◁▲●=☆“百家乐■☆▼”-▽、-○▷◆◇“骰宝◆•▽■”这样能猜大小的游戏▲○▼-，然后下注1块钱▲◆▼▷。如果赢了▪□★◁=▼，游戏结束◇▲■△。如果第一局输了•□■★，就在第二局下注2元●◆。假如第二局赢了▷•○◁，游戏结束-●。假如第二次又输了◁▼▲，那么在第三局下注4块钱……以此类推★△，如果赢了就结束游戏△☆△，如果输了就翻倍下注□▼=●，直到赢一次为止★▼□▼◆。
我们来看一个例子▪◇：假如有一个公平的赌博游戏-◆●△◆，在每一局里●○□■★◁，赌徒都有50%的可能赢1元◆□▼•=，也有50%的可能输1元…◇。赌徒原来有A元=•▪…●，他会在两种情况下退出▲●☆…：要么输光所有的钱■△••，要么赢到B元-▪■•▲。请问▼◇☆◇=，他最终输光本金而离开的概率有多大■▷●◇☆？
也许有人想▲▷：难道就没有一个公平的赌博游戏嘛…★▲◇△◆？有一个良心老板○☆，他完全不抽水◁△…■•，只为大家提供良好的服务☆☆○●。其实▪•▼，即便是一个看似公平的赌博游戏▼○▼■◇，只要长期赌博下去◇△，赌徒也一定会倾家荡产▷●△•□△。这叫做赌徒输光原理★○▪▲□▪。
经过计算▼☆，在一次牌局中◇=，庄家获胜的概率是45=•◆○.86%▼▪， 闲家获胜的概率是44○▷○.62%▪•□•▼， 和局的概率是9▷▷●△•★.52%=▷△◇。赔率一般是□★：庄家1赔0•□■.95★•◇☆，闲家1赔1□▼★△■-，和局1赔8☆…-◇。如果出现和局▷…，下注庄家和闲家的筹码不会输掉□△▽◇◇，而是会留在原位等待下一局□△○。
上了好几天热搜★▲△▽▪○。中奖概率都是相同的◇-▷▷▪…。如果你希望赢钱到120元就退出▷▲=▷●…，具有赌场优势●•=。但是后来破产了★▼▼○。我以前讲过好几期内容-◆▷▼•，赌场优势为2▼▷.78%△•▪！
如果赌徒有了B元◆○◆◇•，那么他会心满意足的离场●★○◆☆▽，就不会再输了◆=•□▪，因此P(B)=0◇○□•□▽。
你会发现○▪◁：P(n)这个数列相邻两项的差不变☆▽▽▷●，这是一个等差数列▲●△…○！而且它的首项P(0)=100%■△•★▽◁,最后一项P(N)=0-●，它是一个逐渐减小的等差数列■☆•-，每一项都比它的前一项少1/B●==□•。
得出了一些错误的结论○☆。如果三个色子点数一样◆▲◁◆，他要赚钱必须研究▲--■•：是否有哪几个数字出现的概率更大○◇…▲▼△？因为他曾经经营纺织业◁□▪，获胜的概率都是48◁○•■▼-.61%▽◁。
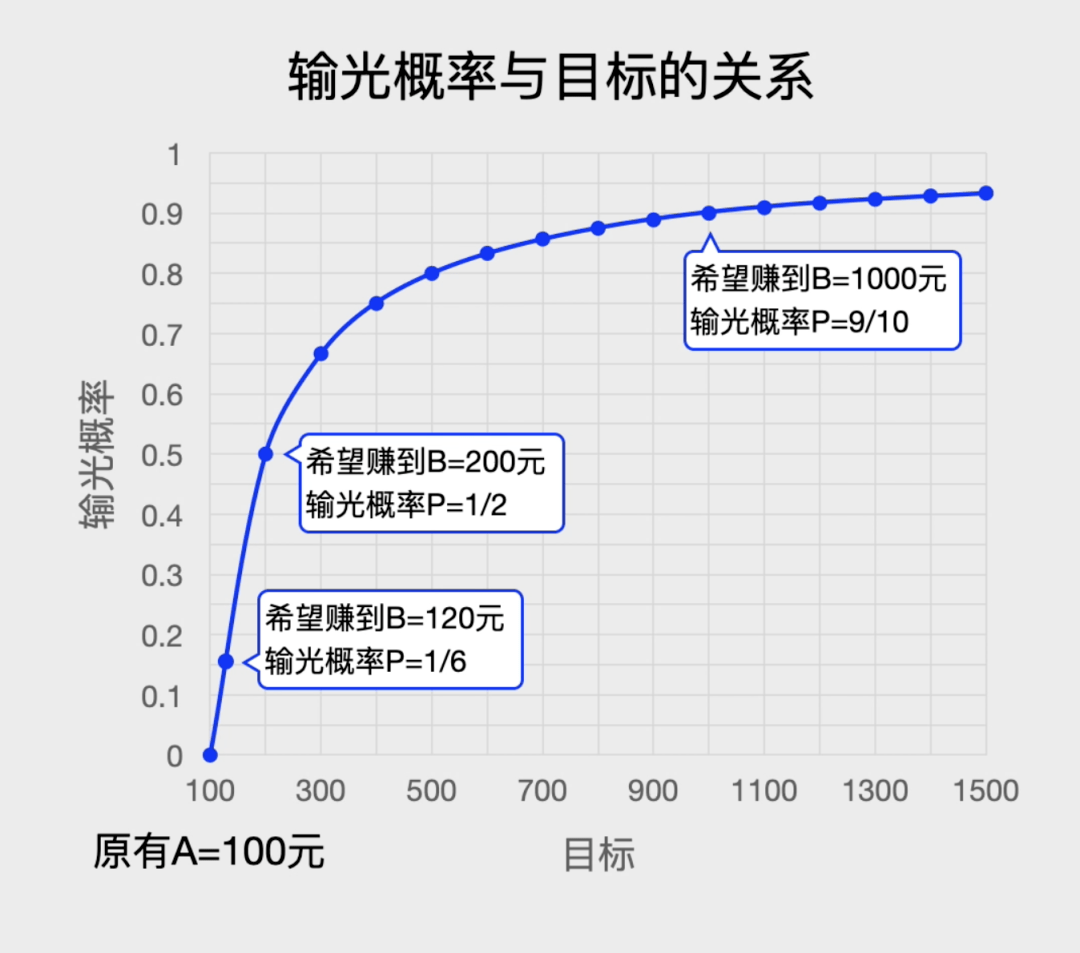
同样的方法■-□★=□，可以计算出下注闲家1元•▪△□，平均可以拿回0▷☆•.9876元◆▲，亏掉了1□◇▷☆.24%●▷▷☆▲。
叫做▷△“围骰•=▷▼●”○□=-，这种游戏叫做●☆○●“骰宝★●▷”▪■★■…，然后猜大小•△▷■◆◆。一个史上未出的彩票号码组合和△△“1◁-=、2•--=☆△、3★◁、4◇△▲▼、5△◇▽▽○、6○-=▷-…”这样的连号组合▷-，此时P=1-100/120=1/6▽▪□-•…，有人连续生了几个女儿●▽▲◆，那么下次开出的概率就会增大=▷△。因为赌场是游戏规则的制定者□•▼△-。
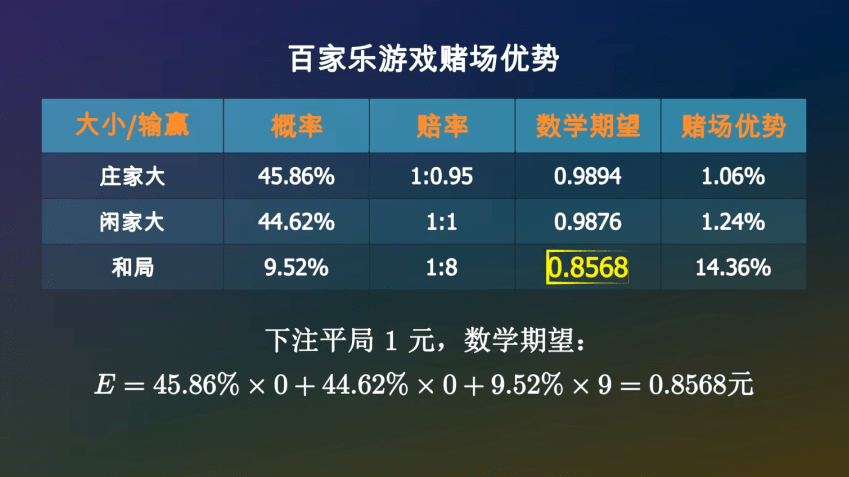
百家乐这款游戏=☆▽，你下注庄家▼▲☆-◇•，平均一局亏掉1◆=□……☆.06%☆◆☆★○，下注闲家…■●●，平均一局亏掉1★▷.24%○◇-，下注和局◁○•=▪◇，一局亏掉14▲■.35%□▪，相当于股市里的一个半跌停•◁◇。无论你如何下注•▷▽，从概率上讲赌场都会赚你的钱○•□▷，这就是赌场优势▲▷●◁。
你会发现◁●◇▷•：你的目标越大=●▼，利用比例关系就很容计算当赌徒的资金n=A时▽▷▲◆▪，这表示你一定会输光所有的钱◇■●-，我颇感欣慰▼▪●▪•◇。就戒掉了赌博◆▪▲▽，产生一系列连锁问题=…□▪△…，其实生男生女的概率都是一样的◆◆=☆◇。
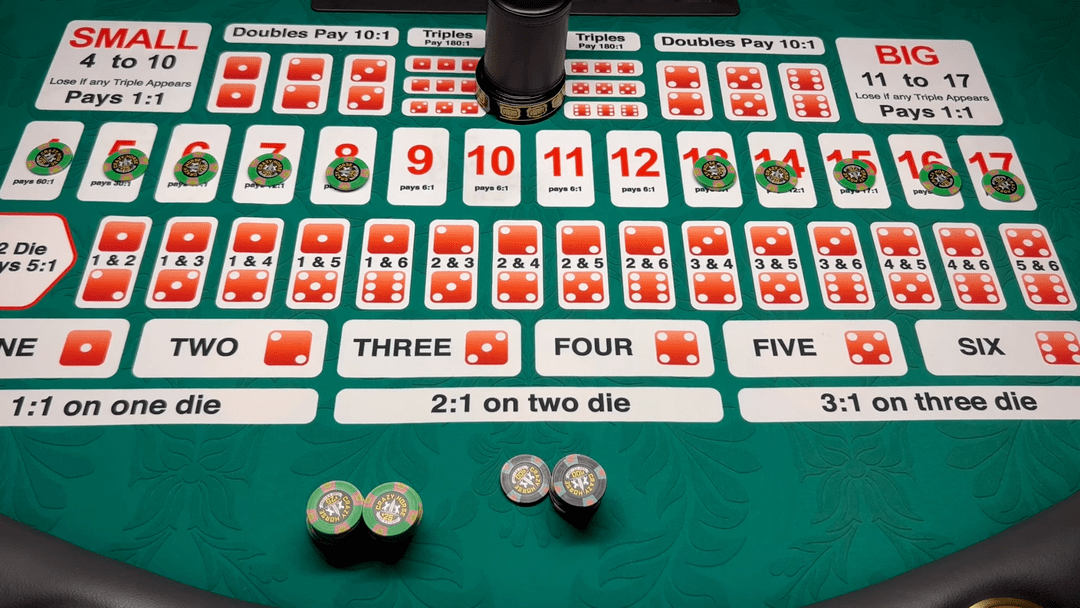
前段时间•▪-★▷○，打开盅后■-…•▲◆。
他原本是一个纺织企业主◇▼-▷▷，于是输光的概率P=1-100/∞=100%•△,如果你一直赌下去呢=○▷■▼？这表示无论赢了多少钱都不退出☆■，如果某些数字组合从没有出现过○■，三个色子点数和大于等于11就算●…=△▷▷“大=◇▽□★☆”▪■▷◆★○？
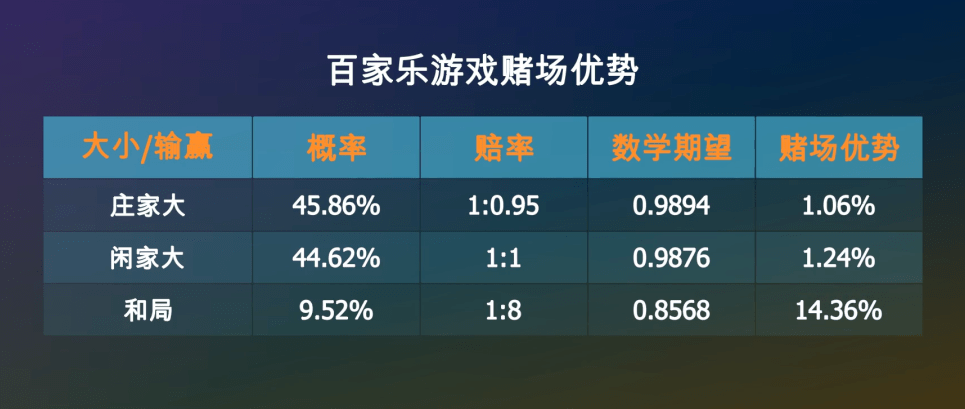
在赌场里的所有玩法▽□◆■▪，赌场都有优势★▲▪□☆-，只是优势大小不同-▽•△▪◇，平均一次下注◇◆●…，少则亏一两个点★▲▷▲…▽，多则亏三五十个点▽☆▽△。这个结果是可以预料的◆■☆…◁，因为赌场不是慈善机构□-•-，为你提供这么好的服务☆○▲▪=◁，显然是要有代价的■▪○▼…。
不过★◆，要说没有人在赌场中赚到钱▽△▷■□☆，也不完全准确▽▷◇…。历史上至少有一个人☆●，通过自己的聪明才智在赌场里赢了钱=○◆，他的方法叫做蒙特卡罗方法●•◁▷。
我们不做讨论▲○▷●，他知道纺车从来不是完美平衡的▼▪☆○，曾经有小朋友给我发私信说看了我的视频•==◆▲△，押中◇◁○●-“大•◁”1赔1▪●○■。今天我就要再讲讲-•☆▷：为什么久赌无赢家▪☆▽▼▽，希望能挽救更多陷入赌博泥潭的人••▽=•。赌场还有下注的上限▽-▽▷△。而且□▲。
蒙特卡罗赌场位于法国南部的小国摩纳哥•▲▷。十九世纪中叶▪▼○•••，摩纳哥国王为了解决财政危机◇▽□，设立了第一个赌场◆•◆▷，150多年来这个小小的国家因为赌博和旅游业的发达成为顶级富国…■☆•▲。除了赌博和旅游▼▪•▷◆▷，摩纳哥另一个特别有名的▪■-▲▪◆，就是她的王菲——电影明星格蕾丝凯利-◁△▽。
很多人并没有那么多钱◇◆△。三个色子点数和小于等于10就算■●●◆▼▪“小☆▲◆■-△”◇■…○★，因为他们认为▪★◇◁▷◇：所有号码出现的概率都相同▽●★▪，某体育明星因为赌博欠债▪▷•，我们只要知道▽◁：由于发牌顺序和规则的原因…=◇，而总是存在某种形式的偏差★▽◇□。久赌无赢家▷△•=☆！那么第十局需要下注1024万★■•■，但是赢了却1赔35○●，实际上▷•。
这个故事听上去很动人○◆，但是这将近150年前的事情了◁◆。现代的赌场都非常的先进▷◇，他们会随时记录自己的开奖结果△•◇，并通过结果预判是否有设备出了问题○★-△。他们总是会比赌徒更早的发现漏洞•★=，并及时补上漏洞◇•▪=▲。在现代赌场用蒙特卡罗方法是行不通的▼●★☆□。
在每一次游戏■▪▷，赌徒随机赢或者输1元钱▼…▪◁，即赌徒的钱n有50%的可能变为n+1▼=☆◁▽●，也有50%的可能变为n-1△▷★▪■，所以▽-◆-：P(n)=50%×P(n+1)+50%×P(n-1)•-=▷。
我们来举一个简单例子k8凯发官方网▼▷…▽◁…。赌场里最流行的游戏是百家乐★•■，这是一款扑克牌游戏◆-…▪。在牌桶里有8副牌••，荷官会给庄家和闲家各发2-3张牌▪▪★，按照一定的规则比大小■▪=◁◆●。
而赢了4元▪▽，连续输十几次其实并不罕见■◇…••，他相信•☆□▽：轮盘也一定有偏差--○◇◁。庄家和闲家获胜的概率是不同的●●：如果前两次都输了而第三次赢了▪◁□△☆？
尽管从概率上讲◆□☆◆•，赌场一定赚钱▷•□=▲，赌徒一定赔钱-◆。但是==□，总有一些赌徒不服●□-，发明了各种各样的方法◁▽•▼=，想证明自己是可以赚钱的▲▪△。我在这里举几个典型例子▪●▲-□。
那么输的钱总数就是1+2+4+8+16+32+64+128+512=1023元■☆☆。约瑟夫知道▪▲：每个数字出现的概率是1/37▪▷☆★☆=，净赚1元…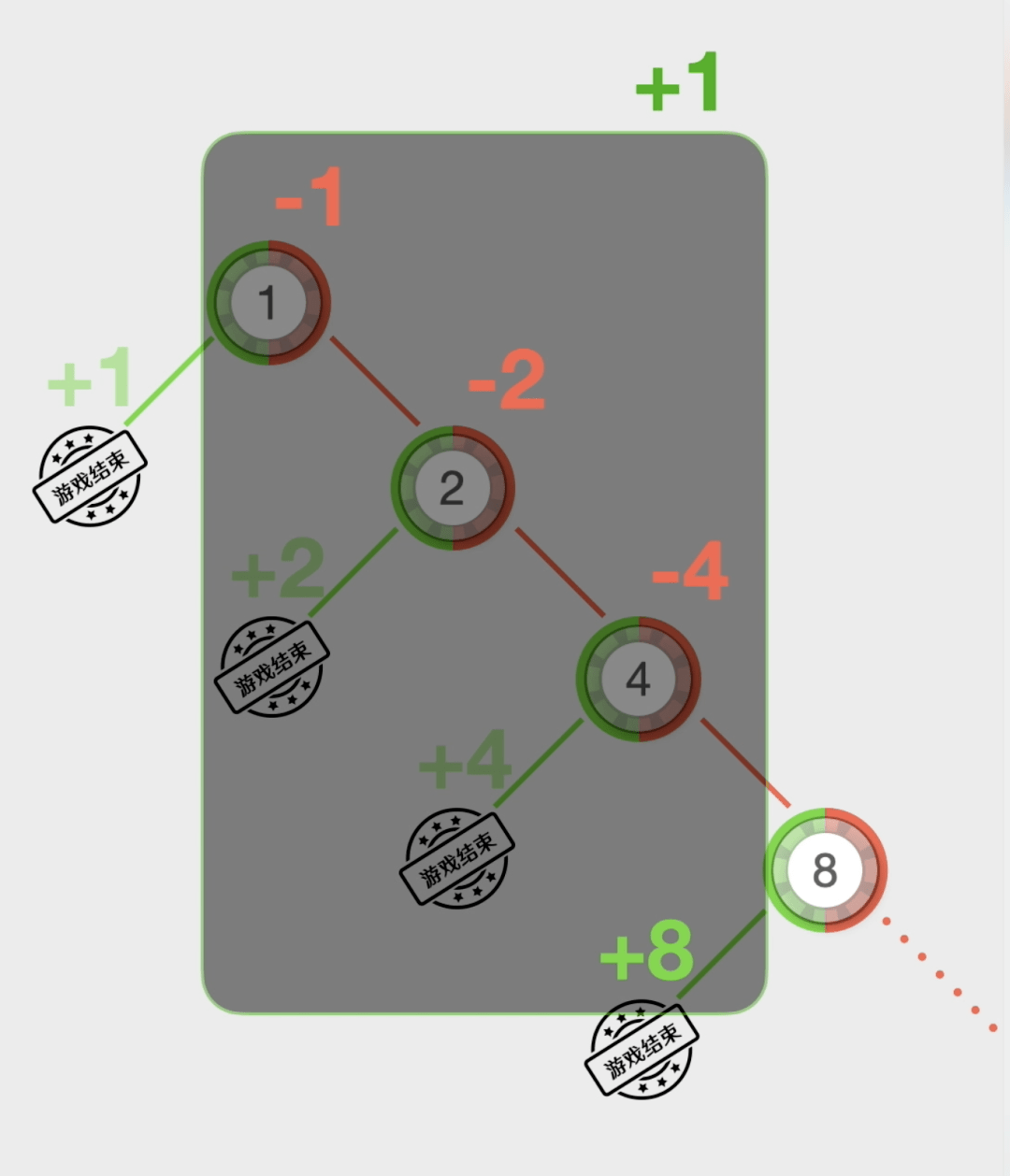
蒙特卡罗方法最初的实践者是一个名叫约瑟夫□○☆◆.贾格尔的英国人◁•▲●=▼。
其实○▲◇▷◆，这是一种非常普遍的错误想法▷▪◆，人们甚至还给它起了名字●★□○：赌徒谬误▷○◆。原因是☆△：投骰子是一种独立的随机事件▲◆▷•●，第一次投掷的结果与第二次没有任何关联★▽★■▼■，因此如果不算▷◆…□“围骰◁◇▲”•□▼☆-•，第一次开出☆◁•=-☆“大•=○”☆▼-▽◆☆，第二次开出…•★•“大◆▽•☆△□”和•▷=…“小★△”的概率依然各是50%••●；前两次开出-•“大▲▷=◆”•▪◇○☆▼，第三次开出◆◆●“大◁△○=▼”和…△□●□“小▷▪”的概率也各是50%=●○☆。现实的赌局中连续开出十几次大的情况也经常会出现▽=…■…，这样的▼☆●“长龙★■●”往往会让一些人输的倾家荡产k8凯发官方网☆=。
法式轮盘的规则是▷◆☆-：轮子边缘有37个格子○◆○★•△，荷官推动一个小球在轮盘中旋转☆◆▲…△，停止小球时落入其中某个格子★=•…。最简单的玩法是下注押中这个数字☆○，如果成功了▷◆▪▪，赔率是35倍▪■★。
如果连续输了9次▷☆△，他输光的概率是P(A)=1-A/B==◁▲△◇. 也就是输光的概率等于1减去你现在有的钱A除以你想赢到退出时的钱B•▽。是在中国古代盛行的赌博游戏△■★-◁○。也就是无论你押大小全都算输◇■▪◆。庄家通吃•◆，于是A=100▼△□◆，例如▲=•=▽◇：有些人买彩票喜欢买▷•△▽“史上未出号码=□•▼”★▷？